This code run Multi-class Cascaded T-linkage on a sample instance of the Adelaide Cube HF dataset. It is aimed atthe simultaneous estimation of fundamental matrices and homographies from sparse stereo-correspondences.

Contents

load data

%rng(0); % for debug
sequencename = 'breadcube_FH';
load(sequencename);

% show input data
figure;
display_correspondences(y,G,img2);
hold on;
scatter(y(4,G==0), y(5,G==0),'xk');

Figure shows the input data, outliers are marked with black corsses

fit fundamental matrix

fit the more general model, in this case represented by fundamental matrix (other models availbale are cirlce, line,line from circle, parabola, homography, affine fundamental)

% Sampling parameters
opts1.epsi = 0.035;                    % inlier threshold
opts1.model = 'fundamental';           % model type
opts1.sampling ='localized';           % ( 'uniform' or 'localized' or 'neigh' )
opts1.m = 3000;                        % number of sampled hyphotesis
opts1.geo =1;
opts1.robust = 'x84';
opts1.voting = "gaussx84";             % voting function (try also 'gauss' to limit the influence of the inlier threhsold)



% Hyphoteses sampling
Y1 = sampler_homof(X,opts1);
% T-Linkage clustering
C1 = tlnkg(Y1.P);
% Outlier rejection
C1 = prune_unstable_points( X,C1, @recover_fundamental, @res_fm, 7, opts1.epsi);
% outlier rejection based on NFA is also possible
%kappa = 50;
%C1 = prune_nfa(X,C1, @recover_fundamental, @res_fm, 8, opts1.epsi, kappa );
M1 = recover_fundamental(X,C1);

figure;
display_correspondences(y,C1,img2);

Figure shows the structures related to fundamental matrix models

fit nested models

opts2.epsi = 0.01;
opts2.model = 'homography_from_fund';
opts2.sampling ='localized';
opts2.geo =1;
opts2.m = 500;
opts2.robust = 'off';
opts2.voting = 'gaussx84';

C2 = cascaded_tlnkg_fund(X, C1,M1, opts2);

C2 = prune_unstable_points( X,C2, @recover_homography, @res_homography, 4, opts2.epsi);
%C2 = prune_nfa(X,C2, @recover_homography, @res_homography, 4, opts2.epsi, kappa );
M2 = recover_homography(X, C2);
C2 = stabilize_homo_segmentation(X,C1,C2,M2);

figure;
display_correspondences(y,C2,img2);
title('Inlier of the nested structures');

Figure displays structures related to homgraphies compatible with the previous attained fundamental matrices.

model selection

The main idea is that models belonging to different classes compete with each other only if they explain the same points and are geometrically compatible. In this way, all the intra-class model selection problems are implicitly dealt by T-linkage, whereas the inter-class model selection issues take explicitly the form of one-vs-many or one-vs-one model comparison. Here GRIC is used to compare a fundamental matrix against one or more homographies.

In the GRIC score 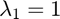$\lambda_1 = 1$ relates to goodness of fit, 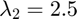$\lambda_2 = 2.5$ relates to model complexity.

lambda1 = 1;
lambda2 = 2.5;

Mu = M1;
Mv = M2;
Cu = C1;
Cv = C2;
num_u = size(Mu,2);
num_v = size(Mv,2);
T = zeros(num_u,num_v);
for i =1:num_u
    for j = 1:num_v
        % if the i-th U and the j-th V have non empty intersection
        % (in this case the compatibility is enforced by construction,
        % otherwise it should be enforced here).
        if(sum((Cu == i).*(Cv == j))>=1)
            T(i,j) = 1;

        end

    end
end


flg_u = true(1,max(Cu));
flg_v = true(1,max(Cv));

[~,resi_fm,~] = recover_fundamental(X,C1);
[~,resi_h,~] = recover_homography(X,C2);
sigma_fm = max(resi_fm);
sigma_h  = max(resi_fm);
for i = 1:size(T,1)

    res_u = res_fm(X(:,Cu==i), Mu(:,i));
    cost_u = compute_gric(res_u.^2,sigma_fm,lambda1, lambda2, 'fundamental');

    if(sum(T(i,:))>0)
        res_v =  inf*ones(size(res_u));
        tail = 1;
        for j= 1:size(T,2)
            if(T(i,j)==1)
                nv = sum(Cv==j);
                res_v(tail: tail+nv-1) = res_homography(X(:,Cv==j),Mv(:,j));
                tail = tail+nv;
            end
        end
        Jv = sum(res_v.^2);

        heta = sum(T(i,:));
        cost_v = compute_gric(res_v.^2,sigma_h,lambda1, lambda2, 'homography',heta);

        if(cost_u < cost_v)
            flg_v(T(i,:)==1)= false;
        else
            flg_u(i)= false;
        end

    end
end


% update labeling

cont = 1;
F = zeros(size(G));
for i = 1:numel(flg_u)

    if(flg_u(i))
        F(Cu==i)=cont;
        cont = cont+1;
    end
end

for i = 1:numel(flg_v)
    if(flg_v(i))
        F(Cv==i)=cont;
        cont = cont+1;

    end
end

result

[miss , fnr, acc, gtgamma] = compute_me(F,G);
fprintf('miss error %f \n',100*miss);

figure;
display_correspondences(y,F,img2);

miss error 4.291845

Final segmentation with Fundamental matrix structure and homography structure on the cube face.


Published with MATLAB® R2018b