Multiple Models Fitting as a Set Coverage Problem

L. Magri, A. Fusiello

Overview

This paper casts the multi-model fitting problem in terms of set coverage, deriving a simple and effective method that generalizes Ransac to multiple models and deals with intersecting structures and outliers in a straightforward and principled manner, while avoiding the typical shortcomings of sequential approaches and those of clustering.

Method

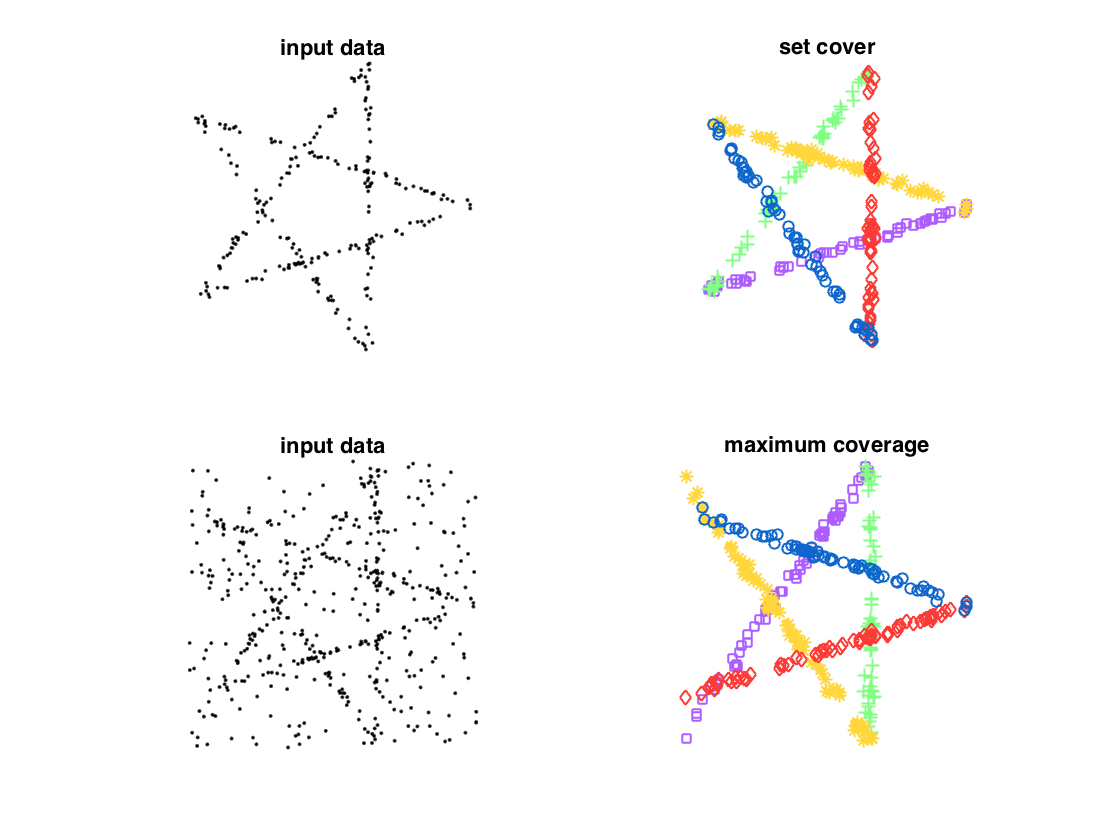
We rely on ``Random sample Coverage'', or RansaCov a simple coverage formulation aimed at retriving from a pool of tentative random models the ones that best explain the data in terms of consensus.
In particular, given the inlier threhshold as input the multi-model fitting problem is resoved via:

Set cover: extract the smallest number of structures whose consenus sets cover all elements
Maximum coverage: search for the largest number of points that can be covered by k consensus sets, possibly leaving some points (the outliers) uncovered.
This method requires to the user to specify as input also the number of desired structures

Both these problems consists in the optimization of a global cost function resorting on consensus, in this way the greediness of techniques such as Sequential/Multi-Ransac and J-linkage are eluded, but at the same time it is also possible to avoid the difficult trade-off between data fidelity and complexity of other formulations.
Note that we do not require the retrived consensus sets to be disjoint, so RansaCov is not limited to partitions and can properly handle the case of intersecting structures.

Code

MATLAB code available: RansaCov code

Reference paper

L. Magri, A. Fusiello. Multiple Models Fitting as a Set Coverage Problem. CVPR16, 2015. (PDF)